C++ Technical Report 1
C++ Technical Report 1 (TR1) is the common name for ISO/IEC TR 19768, C++ Library Extensions, which was a document proposing additions to the C++ standard library for the C++03 language standard. The additions include regular expressions, smart pointers, hash tables, and random number generators. TR1 is not a standard itself, but rather a draft document. However, most of its proposals became part of the current official standard, C++11. Before C++11 was standardized, vendors used this document as a guide to create extensions. The report's goal is "to build more widespread existing practice for an expanded C++ standard library."
Contents |
Overview
Compilers need not include the TR1 components to be conforming, as the TR1 proposals are not yet officially part of the standard. Much of it is available from Boost, and several compiler/library distributors currently implement all or part of the components.
TR1 is not a complete list of additions to the library that appear in the next standard; for example, the current standard, C++11, supports threading. There is also a second technical report, C++ Technical Report 2, planned for publishing after C++11 [1].
The new components are in the std::tr1 namespace to distinguish them from the current standard library.
Components
TR1 includes the following components:
General utilities
Reference wrapper
- based on Boost.Ref [1]
- additions to the
<functional>header file -cref,ref,reference_wrapper - enables passing references, rather than copies, into algorithms or function objects
A wrapper reference is obtained from an instance of the template class reference_wrapper. Wrapper references are similar to normal references (‘&’) of the C++ language. To obtain a wrapper reference from any object the template class ref is used (for a constant reference cref is used).
Wrapper references are useful above all for template functions, when argument deduction would not deduce a reference (e.g. when forwarding arguments):
#include <iostream> #include <tr1/functional> void f( int &r ) { ++r; } template< class Funct, class Arg > void g( Funct f, Arg t ) { f(t); } int main() { int i = 0; g( f, i ); // 'g< void(int &r), int >' is instantiated std::cout << i << "\n"; // Output: 0 g( f, std::tr1::ref(i) ); // 'g< void(int &r), reference_wrapper<int> >' is instanced std::cout << i << "\n"; // Output: 1 }
Smart pointers
- based on Boost Smart Pointer library [2]
- additions to the
<memory>header file -shared_ptr,weak_ptr, etc. - utility for memory management and exception safety using the Resource Acquisition Is Initialization (RAII) idiom
Function objects
These four modules are added to the <functional> header file:
Polymorphic function wrapper
function- based on Boost.Function [3]
- stores all callables (function pointers, member function pointers, and function objects) that use a specified function call signature. The specific type of callable object is not required.
Function object binders
bind- taken from Boost Bind library [4]
- generalized version of the standard
std::bind1standstd::bind2nd - binds parameters to function objects, and allows for function composition.
Function return types
result_of- taken from Boost
- determines the type of a call expression
mem_fn
mem_fn- based on Boost Mem Fn library [5]
- enhancement to the standard
std::mem_funandstd::mem_fun_ref - allows pointers to member functions to be treated as function objects
Metaprogramming and type traits
- new
<type_traits>header file -is_pod,has_virtual_destructor,remove_extent, etc. - based on Boost Type Traits library [2]
- facilitates metaprogramming by enabling queries on and transformation between different types
Numerical facilities
Random number generation
- new
<random>header file -variate_generator,mersenne_twister,poisson_distribution, etc. - utilities for generating random numbers using any of several Pseudorandom number generators, engines, and probability distributions
Mathematical special functions
Some features of TR1, such as the mathematical special functions and certain C99 additions, are not included in the Visual C++ implementation of TR1. The Mathematical special functions library was not standardized in C++11.
These functions will likely be of principal interest to programmers in the engineering and scientific disciplines.
The following table shows all 23 special functions described in TR1.
| Function name | Function prototype | Mathematical expression |
|---|---|---|
| Associated Laguerre polynomials | double assoc_laguerre( unsigned n, unsigned m, double x ) ; | 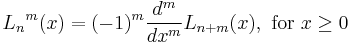 |
| Associated Legendre polynomials | double assoc_legendre( unsigned l, unsigned m, double x ) ; | 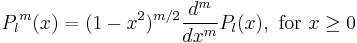 |
| Beta function | double beta( double x, double y ) ; | 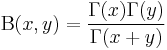 |
| Complete elliptic integral of the first kind | double comp_ellint_1( double k ) ; | 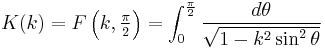 |
| Complete elliptic integral of the second kind | double comp_ellint_2( double k ) ; | 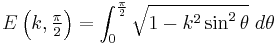 |
| Complete elliptic integral of the third kind | double comp_ellint_3( double k, double nu ) ; | 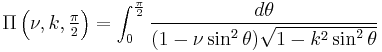 |
| Confluent hypergeometric functions | double conf_hyperg( double a, double c, double x ) ; | 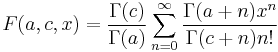 |
| Regular modified cylindrical Bessel functions | double cyl_bessel_i( double nu, double x ) ; | 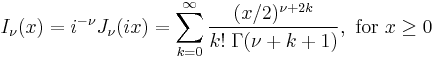 |
| Cylindrical Bessel functions of the first kind | double cyl_bessel_j( double nu, double x ) ; | 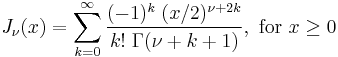 |
| Irregular modified cylindrical Bessel functions | double cyl_bessel_k( double nu, double x ) ; | ![\begin{align}
K_\nu(x) & = \textstyle\frac{\pi}{2} i^{\nu%2B1} \big(J_\nu(ix) %2B i N_\nu(ix)\big) \\
& = \begin{cases}
\displaystyle \frac{I_{-\nu}(x) - I_\nu(x)}{\sin \nu\pi}, & \text{for } x \ge 0 \text{ and } \nu \notin \mathbb{Z} \\[10pt]
\displaystyle \frac{\pi}{2} \lim_{\mu \to \nu} \frac{I_{-\mu}(x) - I_\mu(x)}{\sin \mu\pi}, & \text{for } x < 0 \text{ and } \nu \in \mathbb{Z} \\
\end{cases}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/afe1bce7fc2d8f4c634b8b8814feaf59.png) |
| Cylindrical Neumann functions | double cyl_neumann( double nu, double x ) ; | ![N_\nu(x) = \begin{cases}
\displaystyle \frac{J_\nu(x)\cos \nu\pi - J_{-\nu}(x)}{\sin \nu\pi}, & \text{for } x \ge 0 \text{ and } \nu \notin \mathbb{Z} \\[10pt]
\displaystyle \lim_{\mu \to \nu} \frac{J_\mu(x)\cos \mu\pi - J_{-\mu}(x)}{\sin \mu\pi}, & \text{for } x < 0 \text{ and } \nu \in \mathbb{Z} \\
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/8e366ab40889bc13f751769309f557ce.png) |
| Incomplete elliptic integral of the first kind | double ellint_1( double k, double phi ) ; | 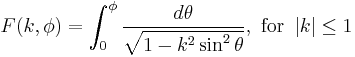 |
| Incomplete elliptic integral of the second kind | double ellint_2( double k, double phi ) ; | 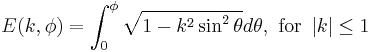 |
| Incomplete elliptic integral of the third kind | double ellint_3( double k, double nu, double phi ) ; | 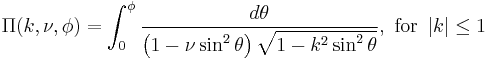 |
| Exponential integral | double expint( double x ) ; | 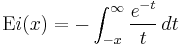 |
| Hermite polynomials | double hermite( unsigned n, double x ) ; | 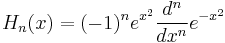 |
| Hypergeometric series | double hyperg( double a, double b, double c, double x ) ; | 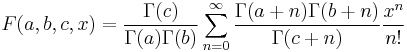 |
| Laguerre polynomials | double laguerre( unsigned n, double x ) ; | 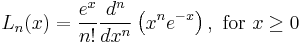 |
| Legendre polynomials | double legendre( unsigned l, double x ) ; | 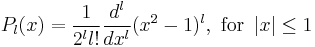 |
| Riemann zeta function | double riemann_zeta( double x ) ; | ![\Zeta(x) =
\begin{cases}
\displaystyle \sum_{k = 1}^\infty k^{-x}, & \text{for } x > 1 \\[10pt]
\displaystyle 2^x\pi^{x-1}\sin\left(\frac{x\pi}{2}\right)\Gamma(1-x)\zeta(1-x), & \text{for } x < 1 \\
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/0770c3b962273c9fc126a401e2bf696a.png) |
| Spherical Bessel functions of the first kind | double sph_bessel( unsigned n, double x ) ; | 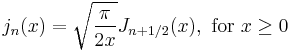 |
| Spherical associated Legendre functions | double sph_legendre( unsigned l, unsigned m, double theta ) ; | ![Y_{l}^{m}(\theta, 0) \text{ where } Y_{l}^{m}(\theta, \phi) = (-1)^{m}\left[\frac{(2l%2B1)}{4\pi}\frac{(l-m)!}{(l%2Bm)!}\right]^{1 \over 2} P_{l}^{m}(\cos \theta)e^{\mathrm{i}m\phi}, \text{ for } |m| \leq l](/2012-wikipedia_en_all_nopic_01_2012/I/da20cfbc07f598887d8bf16f27918824.png) |
| Spherical Neumann functions | double sph_neumann( unsigned n, double x ) ; | 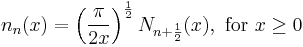 |
Each function has two additional variants. Appending the suffix ‘f’ or ‘l’ to a function name gives a function that operates on float or long double values respectively. For example:
float sph_neumannf( unsigned n, float x ) ; long double sph_neumannl( unsigned n, long double x ) ;
Containers
Tuple types
- new
<tuple>header file -tuple - based on Boost Tuple library [6]
- vaguely an extension of the standard
std::pair - fixed size collection of elements, which may be of different types
Fixed size array
- new
<array>header file -array - taken from Boost Array library [7]
- as opposed to dynamic array types such as the standard
std::vector
Hash tables
- new
<unordered_set>,<unordered_map>header files - they implement the
unordered_set,unordered_multiset,unordered_map, andunordered_multimapclasses, analogous toset,multiset,map, andmultimap, respectively- unfortunately,
unordered_setandunordered_multisetcannot be used with theset_union,set_intersection,set_difference,set_symmetric_difference, andincludesstandard library functions, which work forsetandmultiset
- unfortunately,
- new implementation, not derived from an existing library, not fully API compatible with existing libraries
- like all hash tables, often provide constant time lookup of elements but the worst case can be linear in the size of the container
Regular expressions
- new
<regex>header file -regex,regex_match,regex_search,regex_replace, etc. - based on Boost RegEx library [8]
- pattern matching library
C compatibility
C++ is designed to be compatible with the C programming language, but is not a strict superset of C due to diverging standards. TR1 attempts to reconcile some of these differences through additions to various headers in the C++ library, such as <complex>, <locale>, <cmath>, etc. These changes help to bring C++ more in line with the C99 version of the C standard (not all parts of C99 are included in TR1).
Technical Report 2
In 2005 a request for proposals for a TR2 was made with a special interest in Unicode, XML/HTML, Networking and usability for novice programmers.[3].
Some of the proposals include:
- Threads [4]
- The Asio C++ library (networking [5][6]).
- Signals/Slots [7][8]
- Filesystem Library [9] - Based on the Boost Filesystem Library, for query/manipulation of paths, files and directories.
- Boost Any Library [10]
- Lexical Conversion Library [11]
- New String Algorithms [12]
- Toward a More Complete Taxonomy of Algebraic Properties for Numeric Libraries in TR2 [13]
- Adding heterogeneous comparison lookup to associative containers for TR2 [14]
See also
- C++11, the most recent standard for the C++ programming language; the library improvements were based on TR1
- C99, the most recent standard for the C programming language
- Boost library, a large collection of portable C++ libraries, several of which were included in TR1
- Standard Template Library, part of the current C++ Standard Library
- Dinkumware, the only commercial vendor to fully implement TR1
References
- ISO/IEC JTC1/SC22/WG21 (2005-06-24) (PDF). Draft Technical Report on C++ Library Extensions. http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2005/n1836.pdf.
- Becker, Peter (2006). The C++ Standard Library Extensions: A Tutorial and Reference. Addison-Wesley Professional. ISBN 0-321-41299-0.
External links
- Scott Meyers' Effective C++: TR1 Information - contains links to the TR1 proposal documents which provide background and rationale for the TR1 libraries.
References
- ^ http://www.boost.org/doc/html/ref.html
- ^ http://www.boost.org/libs/smart_ptr/smart_ptr.htm
- ^ http://www.boost.org/doc/html/function.html
- ^ http://www.boost.org/libs/bind/bind.html
- ^ http://www.boost.org/libs/bind/mem_fn.html
- ^ http://www.boost.org/libs/tuple/doc/tuple_users_guide.html
- ^ http://www.boost.org/doc/html/array.html
- ^ http://www.boost.org/doc/libs/1_36_0/libs/regex/doc/html/index.html